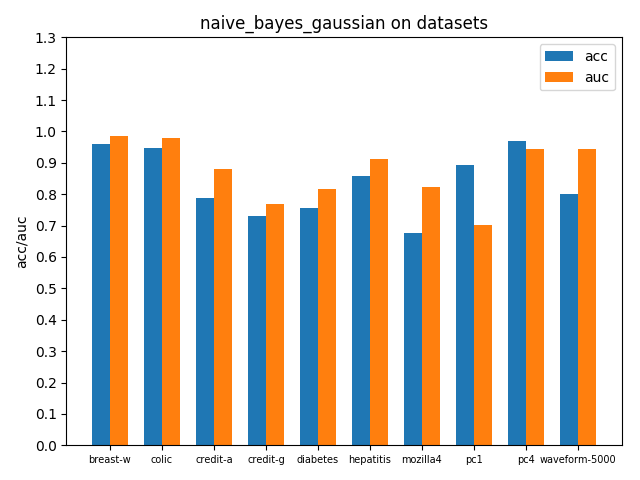
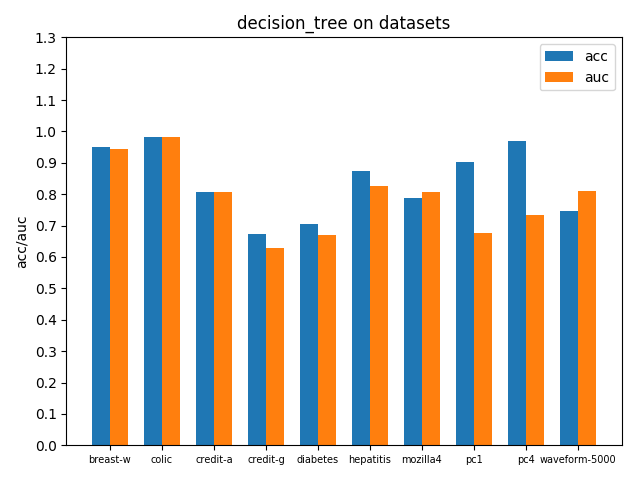
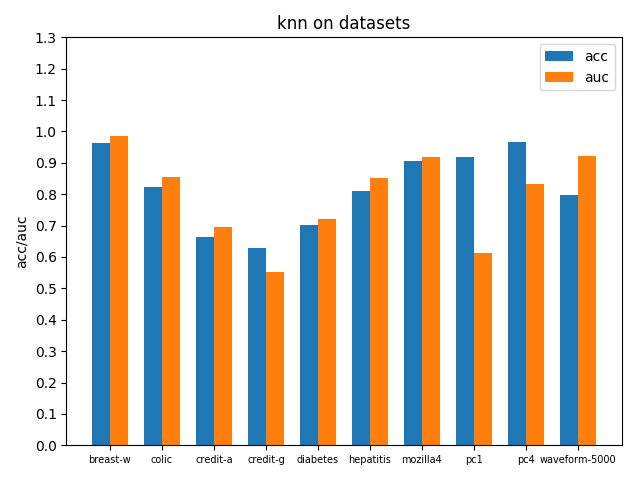
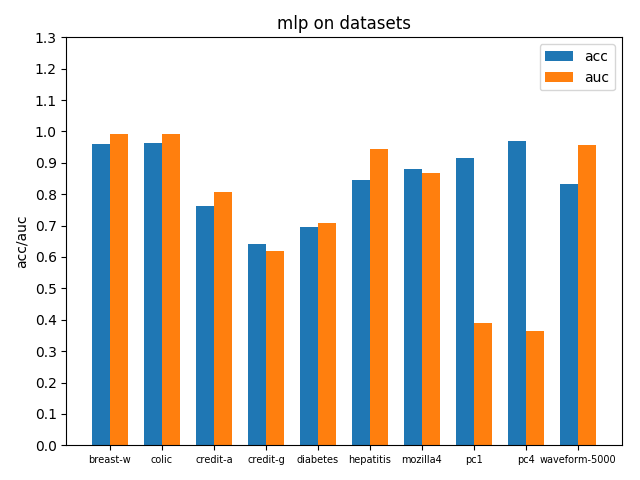
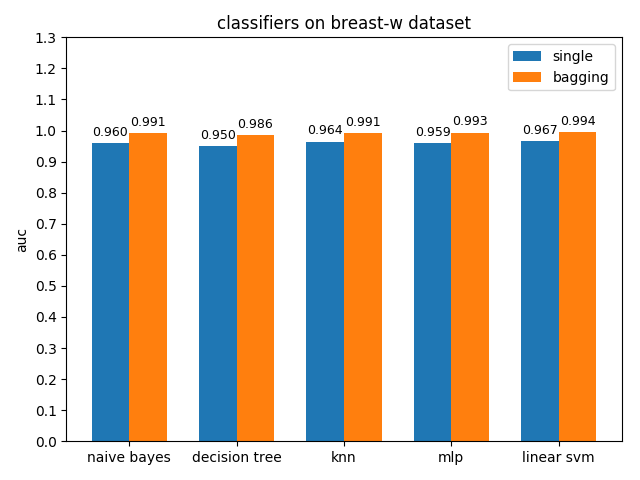
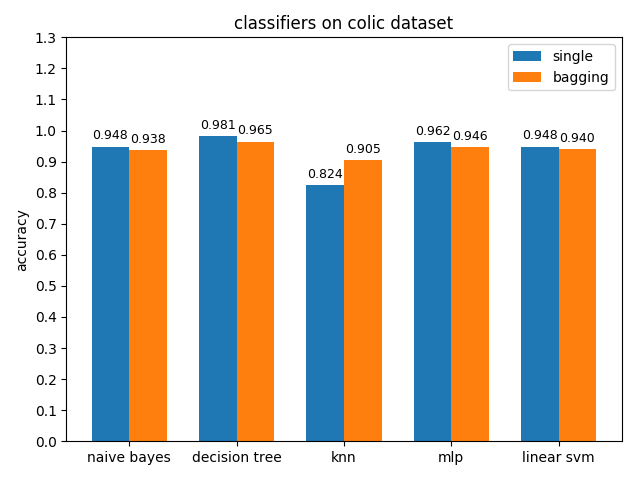
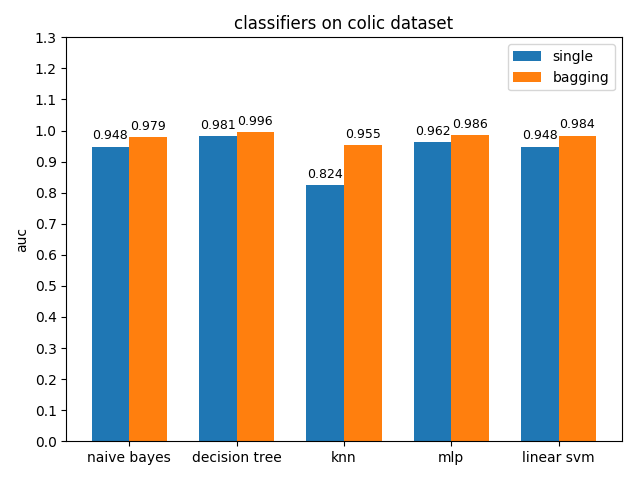
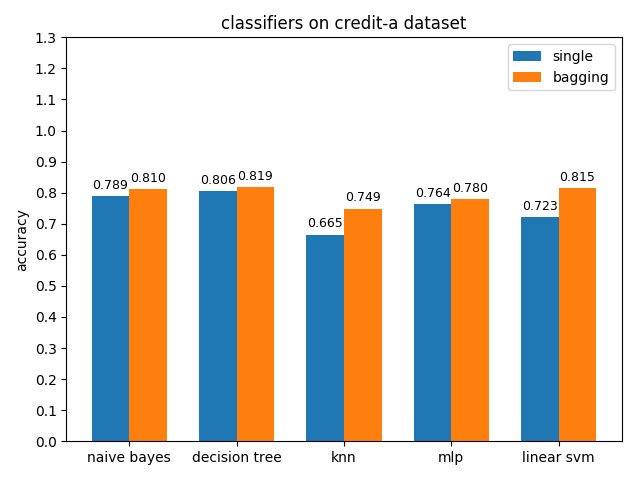
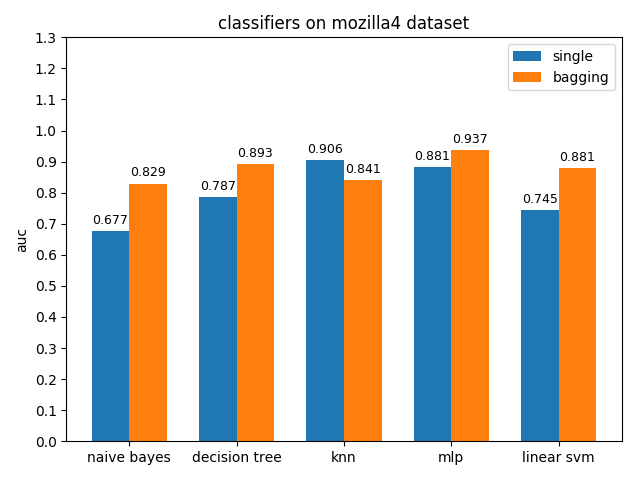
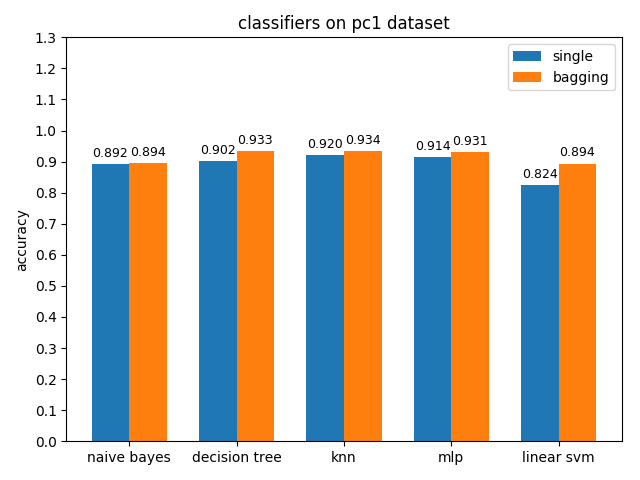
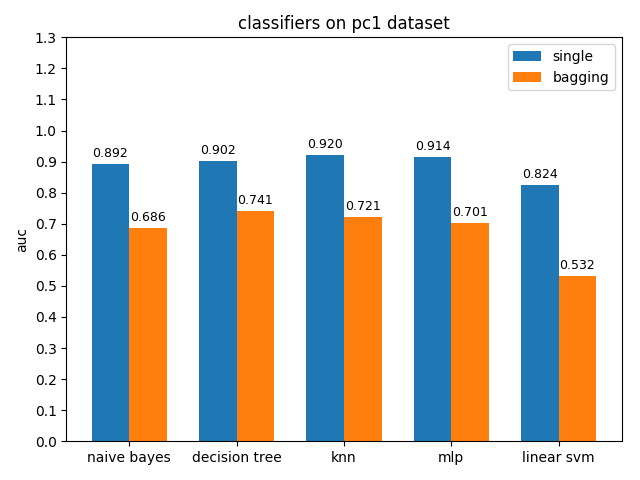
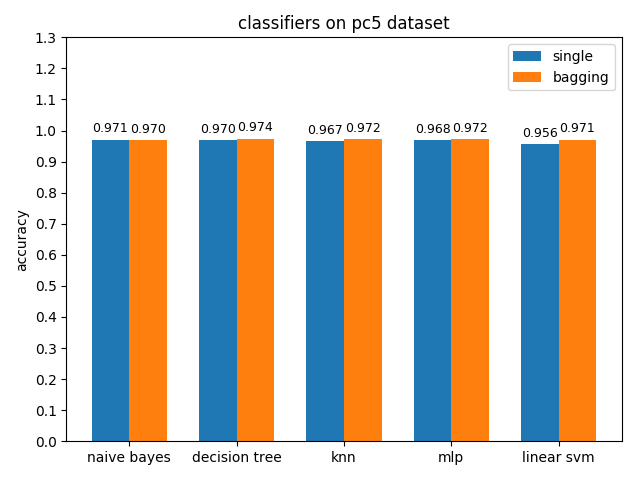
首先看一下三者的定义:
定义1对于图G=(V,E)来说, 最小支配集 指的是从V中取尽量少的点组成一个集合,使得对于V中剩余的点都与取出来的点有边相连。也就是说,设V‘是图G的一个支配集,则对于图中的任意一个顶点u,要么属于集合V’,要么与V‘中的顶点相邻。在V’中出去任何元素后V‘不再是支配集,则支配集是极小支配集。称G的所有支配集中顶点个数最少的支配集为最小支配集,最小支配集中顶点的个数称为支配数。
定义2对于图G=(V,E)来说, 最小点覆盖 指的是从V中取尽量少的点组成一个集合,使得E中所有的边都与取出来的点相连。也就是说,设V‘是图G的一个顶点覆盖,则对于图中的任意一条边(u,v),要么u属于集合V’,要么v属于集合V‘。在V‘中除去任何元素后V’不在是顶点覆盖,则V‘是极小顶点覆盖。称G的所有顶点覆盖中顶点个数最少的覆盖为最小点覆盖。
定义3对于图G=(V,E)来说, 最大独立集 指的是从V中取尽量多的点组成一个集合,使得这些点之间没有边相连。也就是说,设V’是图G的一个独立集,则对于图中任意一条边(u,v),u和v不能同时属于集合V’,甚至可以u和v都不属于集合V‘。在V’中添加任何不属于V‘元素后V’不再是独立集,则V‘是极大独立集。称G的所有顶点独立集中顶点个数最多的独立集为最大独立集。
对于任意图G来说,这三个问题不存在多项式时间的解法。 不过对于树来说,却很容易。目前有两种解法,一种基于贪心思想,另一种基于树形动态规划思想。贪心法能得到具体的点集,而动态规划只能得到集合大小。
一、贪心法
基本算法:
以最小支配集为例,对于树上的最小支配集问题,贪心策略是首先选择一点为根,按照深度优先遍历得到遍历序列,按照所得序列的反向序列的顺序进行贪心,对于一个既不属于支配集也不与支配集中的点相连的点来说,如果他的父节点不属于支配集,将其父节点加入支配集。
这里注意到贪心的策略中贪心的顺序非常重要,按照深度优先遍历得到遍历序列的反向进行贪心,可以保证对于每个点来说,当期子树都被处理过后才轮到该节点的处理,保证了贪心的正确性。
伪代码:
①以1号点深度优先搜索整棵树,求出每个点在深度优先遍历序列中的编号和每个点的父节点编号。
②按照深度优先序列的反向序列检查,如果当前点既不属于支配集也不与支配集中的点相连,且他的父节点不属于支配集,将其父节点加入支配集,支配集中点的个数加1.标记当前节点、当前节点的父节点和当前节点的父节点的父节点,因为这些节点要么属于支配集,要么与支配集中的点相连。
最小点覆盖于最大独立集与上面的做法相似。对于最小点覆盖来说,贪心的策略是,如果当前点和当前点的父节点都不属于顶点覆盖集合,则将父节点加入到顶点覆盖集合,并标记当前节点和其父节点都被覆盖。对于最大独立集来说,贪心策略是如果当前点没有被覆盖,则将当前节点加入到独立集,并标记当前节点和其父节点都被覆盖。
需要注意的是由于默认程序中根节点和其他节点的区别在于根节点的父节点是其自己,所以三种问题对根节点的处理不同。对于最小支配集和最大独立集,需要检查根节点是否满足贪心条件,但是对于最小点覆盖不可以检查根节点。
具体实现:
采用链式前向星存储整棵树。对于DFS(),newpos[i]表示深度优先遍历序列的第i个点是哪个点,now表示当前深度优先遍历序列已经有多少个点了。select[]用于深度优先遍历序列的判重,p[i]表示点i的父节点的编号。对于greedy(),s[i]如果为true,表示第i个点被覆盖。set[i]表示点i属于要求的点集。
最小支配集贪心实现
树上最小支配集贪心完整实现代码如下:
1 |
|
最小点覆盖集贪心实现
对于最小点覆盖集,将greedy函数改为如下:
1 | int greedy() |
最大点独立集贪心实现
对于最大点独立集,将greedy函数改为如下:
1 | int greedy() |
复杂度分析:该方法经过一次深度优先遍历和一次贪心得到最终解,第一步的时间复杂度为O(m),由于这是一棵树,m=n-1.第二步是O(n),总的是O(n)。
二、树形动态规划法
最小支配集树形dp实现
基本算法:
由于这是在树上求最值的问题,显然可以用树形动态规划,只是状态的设计比较复杂。为了保证动态规划的正确性,对于每个点设计了三种状态,这三种状态的意义如下:
dp[i][0]:表示点i属于支配集,并且以点i为根的子树都被覆盖了的情况下支配集中所包含的的最少点的个数。
dp[i][1]:i不属于支配集,且以i为根的子树都被覆盖,且i被其中不少于1个子节点覆盖的情况下支配集中所包含最少点的个数。
dp[i][2]:i不属于支配集,且以i为根的子树都被覆盖,且i没被子节点覆盖的情况下支配集中所包含最少点的个数。
对于第一种状态,dp[i][0]等于每个儿子节点的3种状态(其儿子是否被覆盖没有关系)的最小值之和加1,即只要每个以i的儿子为根的子树都被覆盖,再加上当前点i,所需要的最少点的个数,方程如下:
对于第二种状态,如果点i没有子节点,那么dp[i][1]=INF;否则,需要保证它的每个以i的儿子为根的子树都被覆盖,那么要取每个儿子节点的前两种状态的最小值之和,因为此时i点不属于支配集,不能支配其子节点,所以子节点必须已经被支配,与子节点的第三种状态无关。如果当前所选的状态中,每个儿子都没有被选择进入支配集,即在每个儿子的前两种状态中,第一种状态都不是所需点最少的,那么为了满足第二种状态的定义,需要重新选择点i的一个儿子的状态为第一种状态,这时取花费最少的一个点,即取min(dp[u][0]-dp[u][1])的儿子节点u,强制取其第一种状态,其他儿子节点都取第二种状态,转移方程为:
1 | if(i没有子节点) dp[i][1]=INF |
其中对于inc有:
1 | if(上面式子中的Σmin(dp[u][0],dp[u][1])中包含某个dp[u][0]) inc=0; |
对于第三种状态,i不属于支配集,且以i为根的子树都被覆盖,又i没被子节点覆盖,那么说明点i和点i的儿子节点都不属于支配集,则点i的第三种状态只与其儿子的第二种状态有关,方程为
树上最小支配集树形dp完整实现代码如下:
1 |
|
最终的最小支配集大小为:min(dp[0][0], dp[0][1])
最小点覆盖集树形dp实现
对于最小的覆盖问题,为每个点设计了两种状态,这两种状态的意义如下:
dp[i][0]:表示点i属于点覆盖,并且以点i为根的子树中所连接的边都被覆盖的情况下点覆盖集中所包含最少点的个数。
dp[i][1]:表示点i不属于点覆盖,并且以点i为根的子树中所连接的边都被覆盖的情况下点覆盖集中所包含最少点的个数。
对于第一种状态dp[i][0],等于每个儿子节点的两种状态的最小值之和加1,方程如下:
对于第二种状态dp[i][1],要求所有与i连接的边都被覆盖,但是i点不属于点覆盖,那么i点所有的子节点都必须属于点覆盖,即对于点i的第二种状态与所有子节点的第二种状态无关,在数值上等于所有子节点的第一种状态之和。方程如下:
对于最小点覆盖集实现,将DP函数改为如下:1
2
3
4
5
6
7
8
9
10
11
12void DP(int u,int p) {
dp[u][0] = 1;
dp[u][1] = 0;
int k, to;
for(k = head[u]; k != -1; k = edge[k].next) {
to = edge[k].to;
if(to == p) continue;
DP(to, u);
dp[u][0] += min(dp[to][0], dp[to][1]);
dp[u][1] += dp[to][0];
}
}
最终的最小点覆盖集大小为:min(dp[0][0], dp[0][1])
最大点独立集树形dp实现
对于最大独立集问题,为每个节点设立两种状态,这两种状态的意义如下:
dp[i][0]:表示点i属于独立集的情况下,最大独立集中点的个数。
dp[i][1]:表示点i不属于独立集的情况下,最大独立集中点的个数。
对于第一种状态dp[i][0],由于点i属于独立集,他的子节点都不能属于独立集,所以只与第二种状态有关。方程如下:
对于第二种状态,点i的子节点可以属于独立集,也可以不属于独立集,方程如下:
对于最大点独立集实现 ,将DP函数改为如下:
1 | void DP(int u,int p) { |
最终的最大点独立集大小为:max(dp[0][0], dp[0][1])